Exercise (Week 7)

The queen is the most powerful piece in the game of chess. When a queen is placed in one of the squares of the chessboard, it is able to threaten any number of squares vertically, horizontally or diagonally (corner-by-corner) along a straight line, as follows:

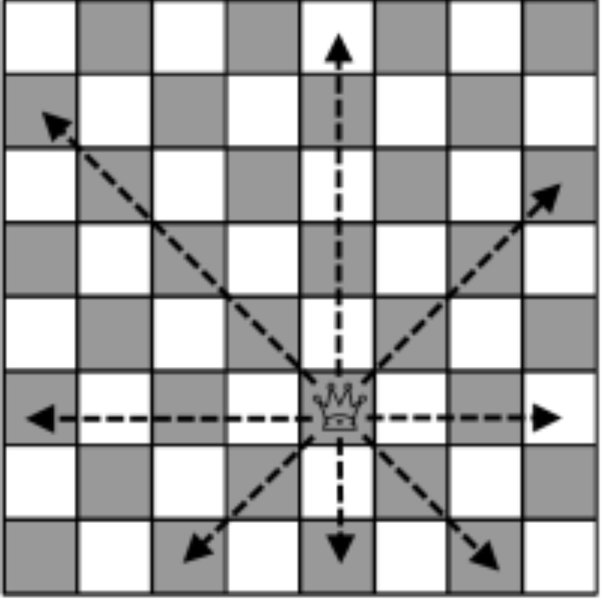
The eight queens puzzle is a famous exercise in both chess and computer programming: the goal is to arrange eight queens on the chessboard in such a way that no two of the queens threaten each other's location.

In a valid solution of the eight queens problem, no two queens can share the same row, the same column, or the same diagonal. Since a chessboard has exactly eight columns, each column must therefore contain exactly one queen.

a. Your first task is to define a function extend that takes in the locations of n queens placed on the first n columns of the board, and places, in all possible ways, a queen on the ~n+1~st column, so that no two of the queens threaten each other.

b. Your second task is to implement a function solutionStartWith which, given the location l of a queen in the first column of the board, returns all possible complete solutions to the eight queens problem in which the queen on the first column occupies the same location l.

Reverse Polish notation (RPN) is a way of writing arithmetic expressions unambiguosly without parentheses. Apart from the lack of parentheses, its main advantage is that it's easy to type into a calculator. Handheld RPN calculators were very popular throughout the 1980s, and some people still swear by them.

Generally, evaluation on an RPN calculator proceeds by maintaining a stack of numbers, and handling each user action separately, as follows:

1. If the user entered a number (e.g. action Enter 5), we push the entered number onto a stack.
2. If the user pressed the button for an arithmetic operation, say +, we remove the two topmost numbers x and y from the stack, and put the result of the operation (in this case y + x) on the stack.
3. There are special buttons: Clear, which, when pressed, removes the topmost number from the stack; AllClear, which removes everything from the stack, and Swap, which swaps the two topmost elements on the stack.

Old calculators could store only 4-5 elements on their stack. Here, we allow our stack to be an unbounded list of numbers. The bottom of the stack is always padded with zeroes: so the stack [] and the stack [0,0] behave identically, as the stacks [5,4] and [5,4,0] behave identically as well. You can play with a simulated RPN calculator by clicking here.

As an example, the following sequence of actions: [Enter 3, Enter 7, Enter 5, Arith (-), Arith (*)] will result in the following final stack state: [6]. First, 3, 7 and 5 are put on the stack. Then we subtract 5 from 7, leaving 3 and 2 on the stack. Finally, we multiply these two, which yields 6.

In this exercise you will implement a Reverse Polish calculator using the State monad.

Your first task is to implement the pop, swap, allClear and performArith functions (a. to d.), which perform the effects of the user actions described above.

e. Your second task is to implement functions app1 and app, which apply a given sequence of user actions to the stack.

You can submit your exercise by typing:

$ give cs3141 ex05 Ex05.hs

on a CSE terminal, or by using the give web interface. Your file must be named Ex05.hs (case-sensitive!).

A dry-run test will partially autotest your solution at submission time. To get full marks, you will need to perform further testing yourself.